Keys and Addresses

A receiver accepts bitcoins to a public key signed by the spender. In order to spend those bitcoins, the spender must sign the transaction with the corresponding private key.
Public Key Cryptography
Cryptography enables the creation of unforgeable digital signatures based on algorithms like elliptic curve. The private key(k) is a number, picked at random. From the private key, we use elliptic curve multiplication to derive the public key(K).
Asymmetric cryptography is used for it’s ability to generate digital signatures. The signature can be produced by the private key and verified by the public key.
Private Keys
A private key is a 256 bit number picked at random(toss a coin 256 times and you have the binary digits of a random private key you can use in a Bitcoin wallet). It is used to create signatures used to spend bitcoins.
The private key can be any number between 0 and n-1 where n is defined as the order of the elliptic curve.
Elliptic Curve
It is a discrete logarithmic problem as expressed by addition and multiplication of points on the curve.
It is derived by the following function:
The indicates that the curve is defined over the field of integers modulo a prime number also written as , where
Since the curve is defined over a finite field of prime numbers, it looks like a pattern of dots scattered in two dimensions.
In elliptic curve, there is a “point at infinity” that roughly corresponds to zero in real numbers.
Addition
There is also a operator w.r.t elliptic curves.
Given two points and on the curve, the sum of the points is calculated by drawing a line through and and finding the third point where the line intersects the curve. The result of is the reflection of the intersection point across the x-axis.
Special cases that need “point at infinity”:
- = : The line is tangent to the curve at and the result is the point at infinity.
- In some cases( and have same x-coordinate but different y-coordinate), the line is vertical and the result is the point at infinity.
The point of infininty is oftne represented as .
+ =
The elliptic curve addition is associative i.e.
Multiplication
Public Keys
The public key is calculated from: where is the generator point of the curve and is the private key. The generator point is specified as part of the secp256k1 standard. A private key will always generate the same public key.
Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
Gy = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8The reverse operation is called “finding the discrete logarithm” and is computationally infeasible.

Output and Input Scripts
The first version of Bitcoin had payments sent to an output script and spent by an input script.
The earlier version of Bitcoin allowed a spender to enter the receiver’s IP address, but that was later removed for being problematic.Every connection to the IP was given a public key(P2PK).
If Alice had to pay bob, she would construct the following output:
<Bob's Public Key> OP_CHECKSIGThe input script to spend the output would be:
<Bob's Signature>The script is executed by the Bitcoin Scripting Language. The input script and output script are combined in a stack form(input first).
<Bob's Signature> <Bob's Public Key> OP_CHECKSIGRead: A primer on the Bitcoin Scripting Language
If the signature is correct, OP_CHECKSIG will return 1, else 0. The script passes if the stack is empty and the top element is 1. The transaction is valid if all scripts pass.
P2PKH
One of the downsides of using IP addresses was that the receiver had to be online at their IP address and it needs to be accessible from outside world which is not practical.
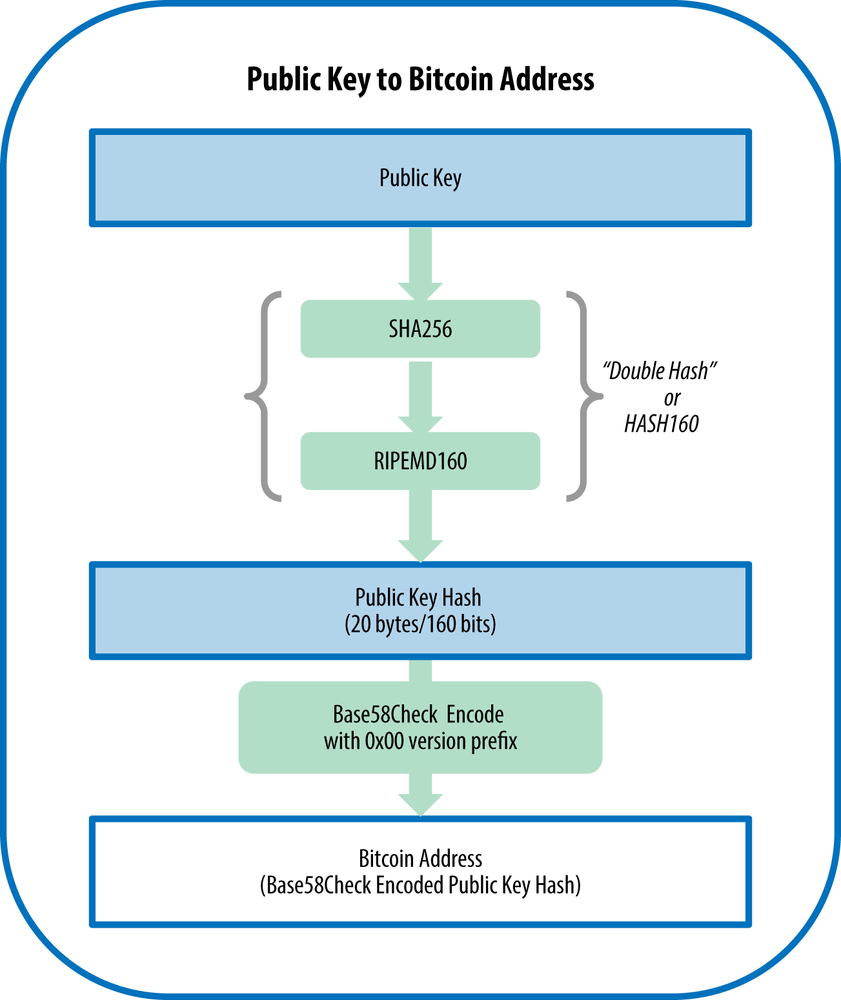
Another problem was having to give receivers a long public key. To solve this, the public key was hashed.
The original version of Bitcoin made commitments to public keys by hashing the key with SHA256 first and then with RIPEMD160 for unstated reasons. This produced a 20 byte commitment.
Usage:
Output Script:
OP_DUP OP_HASH160 <Bob's Hash> OP_EQUALVERIFY OP_CHECKSIGInput Script:
<Bob's Signature> <Bob's Public Key>Together:
<Bob's Signature> <Bob's Public Key> OP_DUP OP_HASH160 <Bob's Hash> OP_EQUALVERIFY OP_CHECKSIGExplanation: First Bob’s signature goes on the stack followed by Bob’s public key. The public key is duplicated and hashed. The hash is compared with the hash in the output script. If the hashes match, the signature is verified. P2PKH allows Alice’s payment to contain only 20 byte commitment instead of 65 byte public key.
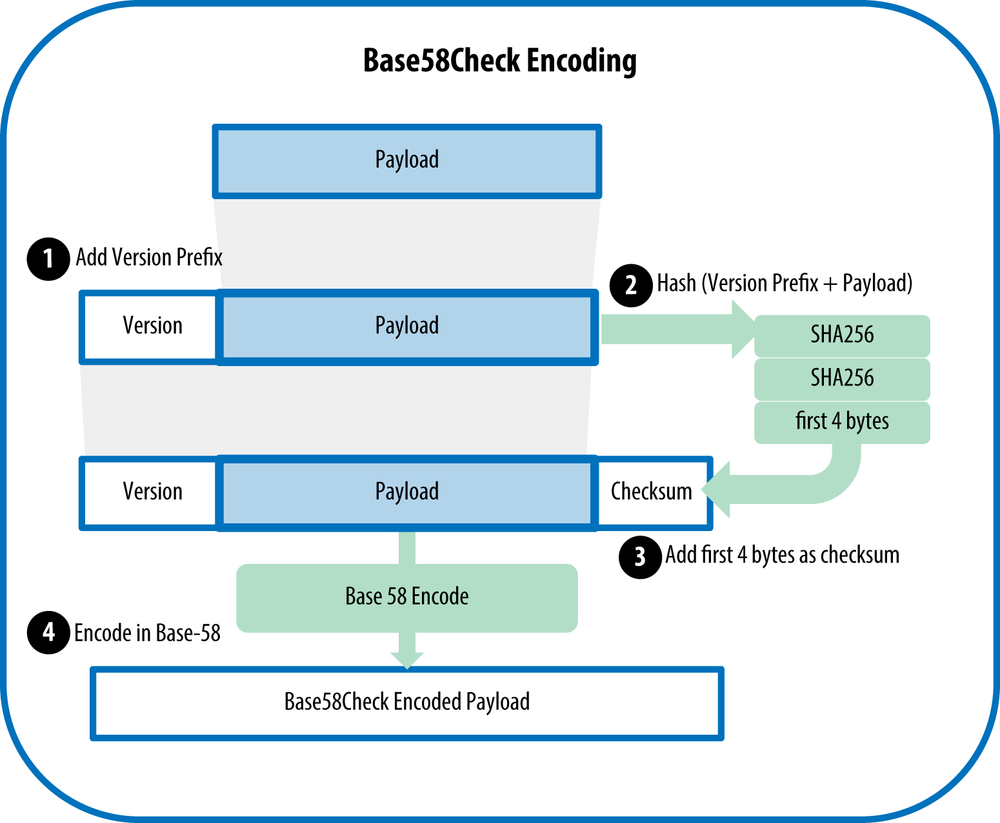
Base58check Encoding
Decimal system uses 10 numerals, hexadecimal uses 16. Similarly base64 uses 64 characters(26 uppercase, 26 lowercase, 10 digits, and 2 symbols). Base58check uses 58 characters(uppercase, lowercase, and digits) excluding 0, O, I, and l to avoid confusion and no symbols. Bitcoin addresses are encoded in base58check.
To convert into base58check we first prefix the date with “version byte”. For example the prefix 0x00 indicates the data should be used as the commitment in a legacy P2PKH output script.
To add extra security against typos, a checksum is added to the end of the commitment. The checksum is calculated by hashing the commitment twice with SHA256 and taking the first 4 bytes of the result. The checksum is appended to the address and encoded in base58.
checksum = SHA256(SHA256(prefix + data))[:4]Result: base58encode(prefix + data + checksum)
| Type | Version prefix (hex) | Base58 result prefix |
|---|---|---|
Address for pay to public key hash (P2PKH) |
0x00 |
1 |
Address for pay to script hash (P2SH) |
0x05 |
3 |
Testnet Address for P2PKH |
0x6F |
m or n |
Testnet Address for P2SH |
0xC4 |
2 |
Private Key WIF |
0x80 |
5, K, or L |
BIP32 Extended Public Key |
0x0488B21E |
xpub |
Compressed Public Keys
The public key is 65 bytes long. The first byte is 0x04 and the next 32 bytes are the x-coordinate and the last 32 bytes are the y-coordinate. The y-coordinate can be calculated from the x-coordinate. If we know the x-coordinate we can calculate the y-coordinate by solving . There are two possible values for y, one even and one odd. The compressed public key is 33 bytes long. The first byte is 0x02 if y is even(in binary) and 0x03 if y is odd. The next 32 bytes are the x-coordinate.
Most Bitcoin wallets use compressed public keys. However wallets still need to support legacy uncompressed public keys so that they can verify older transactions. Failure to scan for both types of public keys can result in loss of funds. To solve this, when private keys are exported, they are exported in a WIF(Wallet Import Format) that indicates that the private key has been used to generate a compressed public key.
Legacy Pay to Script Hash(P2SH)
The reciever can want to put some constraints on how the bitcoins can be spent. Orginially the sontraint was simply that input needs to provide an appropriate signature.
The BIP16 upgrade allowed an output script to commit to a redemption script. In order to spend the bitcions, the spender needs to provide a redeem script that matches this commitment.
Example
Bob wants to require two signatures to spend his Bitcoins.
He creates a redeem script that requires two signatures:
<pubkey 1> OP_CHECKSIGVERIFY <pubkey 2> OP_CHECKSIGBob hashes the redeem script using HASH160 i.e. SHA256(RIPEMD160(redeem script)) and gets the hash:
OP_HASH160 <commitment> OP_EQUALTo spend his bitcoins, bob uses the following input script:
<sig1> <sig2> <redeem script>Full nodes will verify the redeem script by executing it and checking if the hashes match.
The script will be accepted if everything matches and the transaction will pass.
P2SH addresses are also created with base58check. The version prefix is set to 5 which results in an encoded address starting with 3.
P2PKH and P2SH are only ones using base58check and are now replaced by bech32 addresses. There were also probable collision attacks for these addresses.
Bech32 Addresses
One of the advantages of P2SH was that spender didn’t need to know the details of the script the receiver used. The SegWit upgrade was designed to use this mechanism, allowing users to imeediately begin the benefits of P2SH addresses.
Initially it was decided in BIP142 that SegWit addresses would be encoded in base58check. However, it was later decided to use a new encoding called Bech32. Bech32 uses a 32 character set of lowercase letters and digits, excluding 1, b, i, and o to avoid confusion.
Bech32m
There were certain problems with Bech32 addresses. The checksum was not strong enough and there were probable collision attacks. Bech32m was introduced to solve these problems. It uses a different generator polynomial and a different set of constants.
A bech32m address consists of:
- Human-readable part(HRP): The prefix that indicates the network and the type of address.
- Separator: The separator is the number 1.
- Data part: The data part consists of the witness version and the witness program.
- Checksum: The checksum is calculated using the Bech32m generator polynomial.
P2WPKH: The witness program contains a commitment constructed by hashing the public key with SHA256 and then with RIPEMD160.
P2WSH: The witness program contains a commitment constructed by hashing the redeem script with SHA256 only
Private Key Formats
| Type | Prefix | Description |
|---|---|---|
| Hex | None | Raw private key in hexadecimal format |
| WIF | 5 | Base58check encoded with version prefix of 128 and 32-bit checksum |
| WIF-compressed | K or L | Same as WIF with added suffix 0x01 before encoding |
Compressed Private Keys
It is a misnomer. Compressed private keys are one bit longer than uncompressed private keys because it has an extra byte suffix. The suffix indicates that it is from a newer wallet and should only be used to produce compressed public keys.